Less about Numbers, More a Way of Thinking

Chris Thomson describes how maths can illuminate thinking about management:

A recent FE News article on the usefulness of maths reminded me of what I owe to the subject.

To be honest the only time I ever depended on my own maths skills as a college principal was when there wasn’t a mathematician around to help – or when I was on vacation. Pythagoras’ theorem is a great way of estimating the length of a walk when out on the fells. As a friend – really helpfully – suggested: the squall on the high path in use is equal to the sum of the squalls on the other hillsides.

As a former Eng. Lit. student I never actively tried to avoid maths – it just didn’t come easily to me. But then came the day when, newly in post as a vice principal, I found myself responsible for funding and budgeting. Suddenly numbers loomed rather large and proved – shall we say – perplexing.

I would take my mangled calculations along to my colleague Lesley and she would sort them out. And this was how, aged 35, I got a superb maths education. I started seeking Lesley’s advice out of necessity but pretty soon was going back repeatedly because I fell in love with the unfolding of even the simplest maths when it’s done expertly. It’s simply beautiful to behold.

Because I was fascinated, I learned – and principally, three things:

1. Maths makes you ensure information is entire and correct before you try to do anything with it.
2. Maths is only superficially about numbers or symbols. Fundamentally it’s about logical thinking.
3. Maths tries to say something which is universally true rather than something which is true only for a particular case.

I can’t judge whether these points would help would-be mathematicians. All I know is that as a would-be manager they really helped me.

The first two are probably most obviously relevant to decision-making. Getting the basic information straight is critical in an area like HR. Where I might be naturally inclined to start thinking about ‘staffing’, my maths training would intervene: Do you mean support staff or teaching staff? Full-time or part-time? 52 or 44 week contracts?

And checking my thinking for false assumptions and mistaken inferences enabled me to be more confident about conclusions I reached.

Other people might not like them. I might not like them. But we could at least all be sure they were logically sound.

The third point above – reaching for the general case – doesn’t look as if it’s got much to do with management but here’s a practical example of how it actually did. I had been thinking about organisational culture and came up with this:

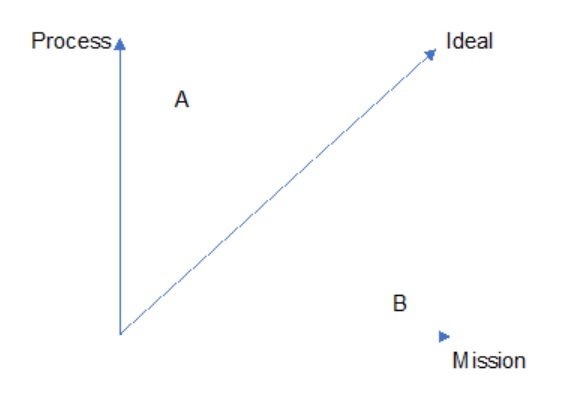
The graph was a way of thinking about a tension between adherence to college processes for their own sake on the one hand, and on the other being guided by the college’s mission without much thought for anyone else. Someone at position A might never put a foot wrong administratively but might also be disinclined to question whether processes needed to change.

Conversely, someone at position B might be an inspirational teacher in the classroom and a nightmare colleague outside it.

Then a futher thought struck me – only as a result of my belated maths education prompting me towards the general case.

What would happen if I extended the axes so the graph looked like this?:

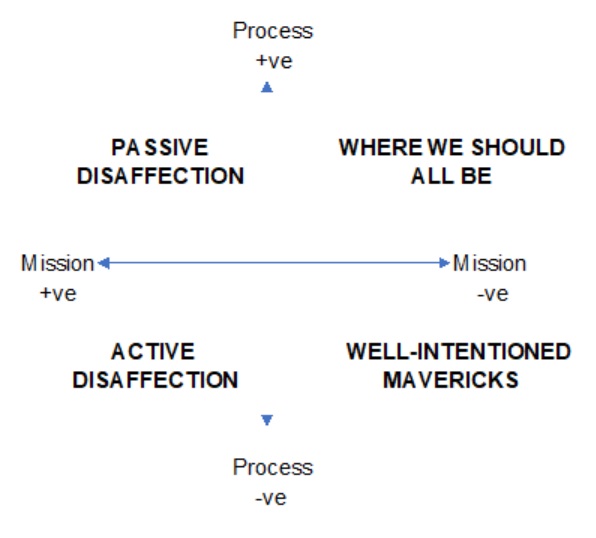
Curiously, an entirely theoretical hunch gave rise to a picture that was truer to life: regrettably we weren’t all in the top right-hand quadrant!

So this example touches on a possible fourth insight: pure maths can describe how the practical world works.

How is that possible? There are answers to this question in the philosophy of mathematics and I could tell you a whole lot more about that.

Just that I’d need to ring Lesley first.